Bildverarbeitung, Mustererkennung, angewandte Informatik

Bei der digitalen Bildverabeitung und Mustererkennung geht es im Prinzip um die maschinelle Verarbeitung visueller Information. Da Computer trotz aller technologischen Fortschritte weit davon entfernt sind mit dem menschlichen Sehapparat vergleichbar zu sein, ist eine Unterstützung durch intelligente Algorithmen notwendig. Das Erlernen und Anwenden - in höheren Semestern auch Entwickeln und Verbessern - solcher Verfahren ist Inhalt von Lehrveranstaltungen der Biomathematik.

Anwendungen von Bildverarbeitung und Mustererkennung finden sich nicht nur in Medizin (Computertomographie, Ultraschall) und Biologie (Strukturerkennung bei Proteinen) sondern beispielsweise auch in der Materialwissenschaft (Texturerkennung), der industriellen Produktkontrolle (Computer Vision) oder der Fernerkundung (Klassifikation).

Beispiel: Segmentierung eines Bildes mit Hilfe von Matlab

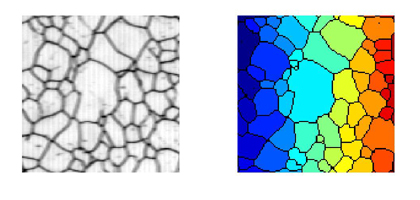
Diese Beispielanwendung ist auch auf der Matlab-Homepage und über die programm-interne Hilfe zu finden ist. Ausgangsbild ist die Aufnahme der zellenartigen Struktur von Stahl. Ziel ist es, die einzelnen Zellen klar, d.h. durch eine 1 Pixel starke Linie abzugrenzen und jede mit unterschiedlichen Farben zu füllen.

Die verwendeten Techniken sind im Grenzgebiet Mathematik/Informatik angesiedelt. Zum einen finden tief liegende mathematische Theorien ihre Anwendung, zum anderen ist der Computer ein unverzichtbares Werkzeug bei der digitalen Bildverarbeitung. Inhalte einer solchen Lehrveranstaltung sind:

· Bei welchen bio-medizinischen Problemen braucht man Bildverarbeitung ?
· Wie kann man digitale Bilder mathematisch modellieren ?
· Welche Information ist im Bild enthalten und wie kann ich sie extrahieren ?
· Wie kann man Bilder verbessern ?
· Wie kann ich Merkmale beschreiben und sie erkennen ?

Die angesprochenen Fragen sind selbstverständlich nicht unabhängig vom untersuchten Bildmaterial. Hat man beispielsweise Satellitendaten akquiriert, so ist der erste Schritt die Rohdaten zu prozessieren, um ein Bild aus ihnen zu machen. Anschließend muß das Bild kalibriert werden, damit die enthaltenen Informationen vergleichbar sind. Dann kann die eigentliche Bildverarbeitung im mathematischen Sinne beginnen. Ähnlich verhält es sich bei der Computertomographie: um die fertigen Schichtbilder zu erzeugen ist eine ganze Menge an Vorverarbeitung und mathematischen Algorithmen notwendig.

Hat man nun ein Bild vorliegen, so sollte man sich zunächst fragen, ob eventuelle Fragen schon im Vorfeld bei der Bildaufnahme gelöst werden können. Die weitere Vorgehensweise hängt nun sowohl von den Daten als auch von der interessierenden Fragestellung ab. Welche Information soll gefunden werden ? Welcher Algorithmus ist geeignet ? Muß das Bild vorverarbeitet werden. Wird beispielsweise ein Röntgenbild mit geringer Dosis aufgenommen, so kann ein solches Bild ‚verrauscht' wirken. Wie man das Rauschen entfernen oder zumindest reduzieren kann ist eine typische Frage aus der medizinischen Bildverabeitung. Dabei muß darauf geachtet werden, daß beim Entrauschen keine interessierenden Strukturen verloren gehen.